SkillsetMaster - AI, Web Development & Data Analytics Courses

Why Spread Matters?

Two datasets can have same mean but look completely different!

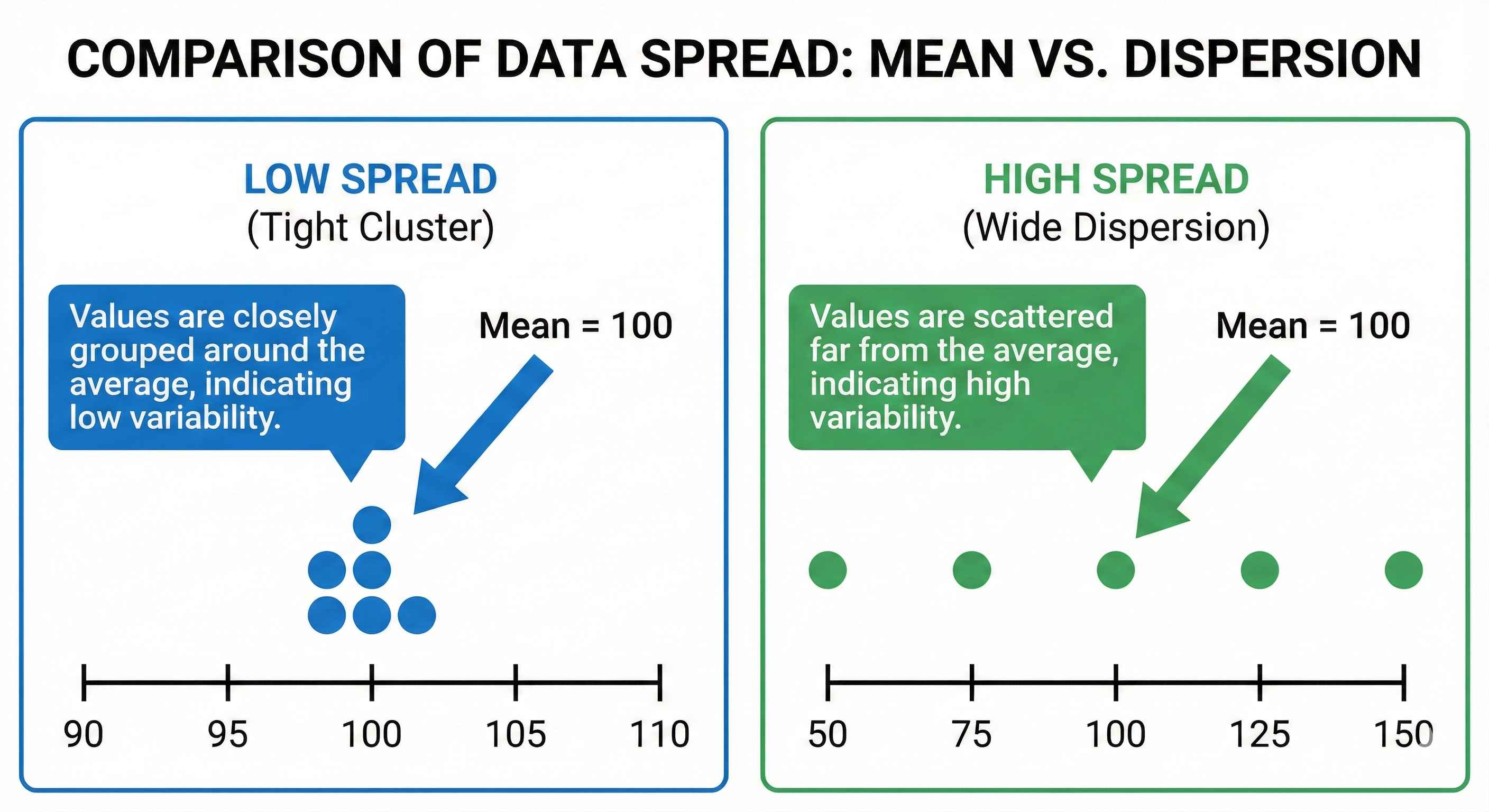
Same Mean Different Spread

Dataset A: 98, 99, 100, 101, 102 → Mean = 100 (tight cluster) Dataset B: 50, 75, 100, 125, 150 → Mean = 100 (wide spread)

Spread tells you how scattered your data is.

1. Range (Simplest)

How: Maximum - Minimum

Example: Data: 10, 20, 30, 40, 50 Range = 50 - 10 = 40

Excel: =MAX(A1:A5) - MIN(A1:A5)

Python:

data = [10, 20, 30, 40, 50]
range_val = max(data) - min(data)
print(range_val)  # Output: 40

Limitation: One outlier can mess up range!

2. Standard Deviation (Most Used)

What it tells: How far values typically are from the mean

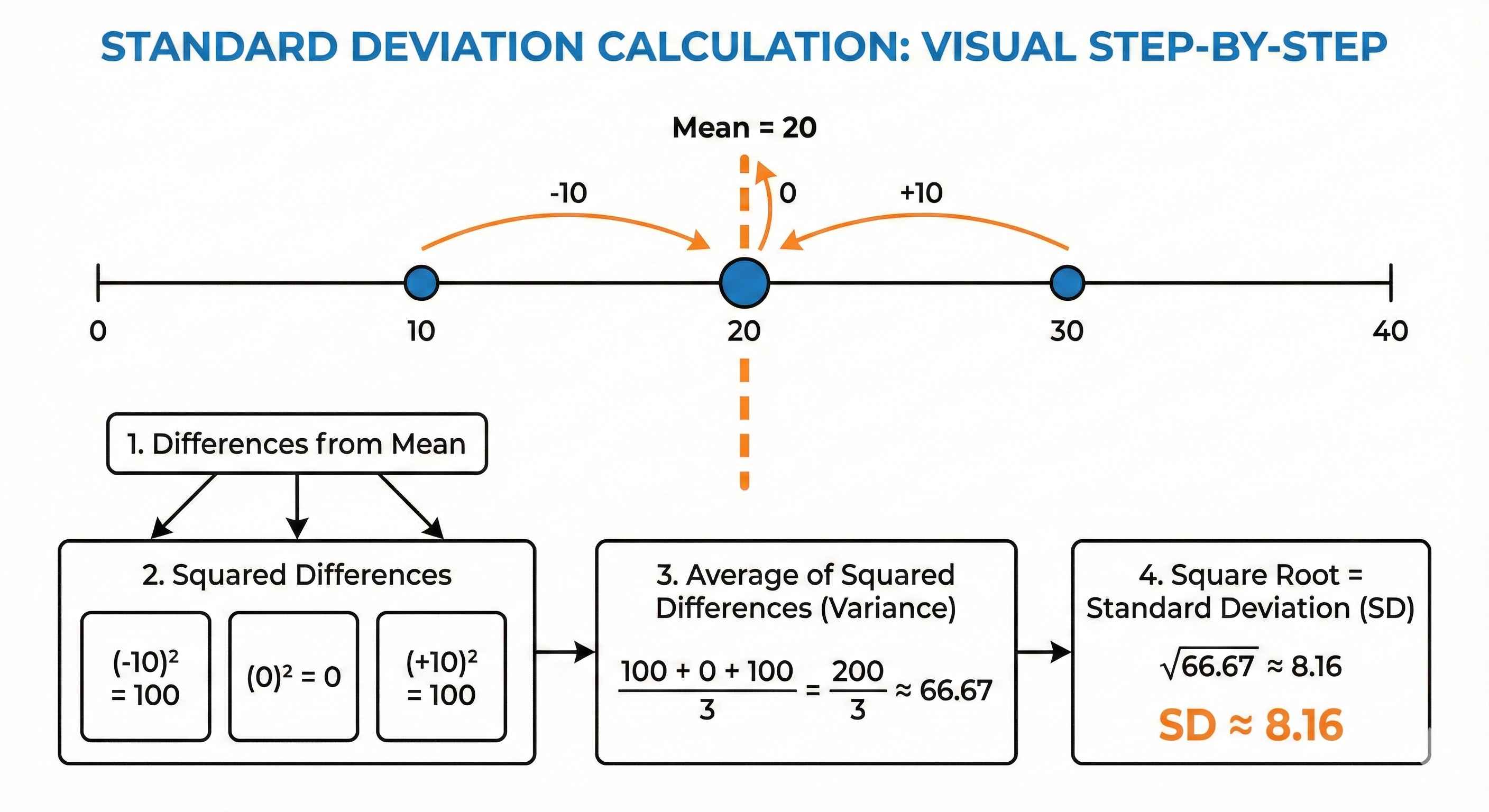
Standard Deviation Explained

Example: Data: 10, 20, 30 (Mean = 20)

Step 1: Find differences from mean → -10, 0, +10 Step 2: Square them → 100, 0, 100 Step 3: Average → 200/3 = 66.67 (this is Variance) Step 4: Square root → √66.67 = 8.16 (this is SD)

Excel: =STDEV.S(A1:A3)

Python:

import statistics
data = [10, 20, 30]
sd = statistics.stdev(data)
print(sd)  # Output: 10.0

3. Interpreting Standard Deviation

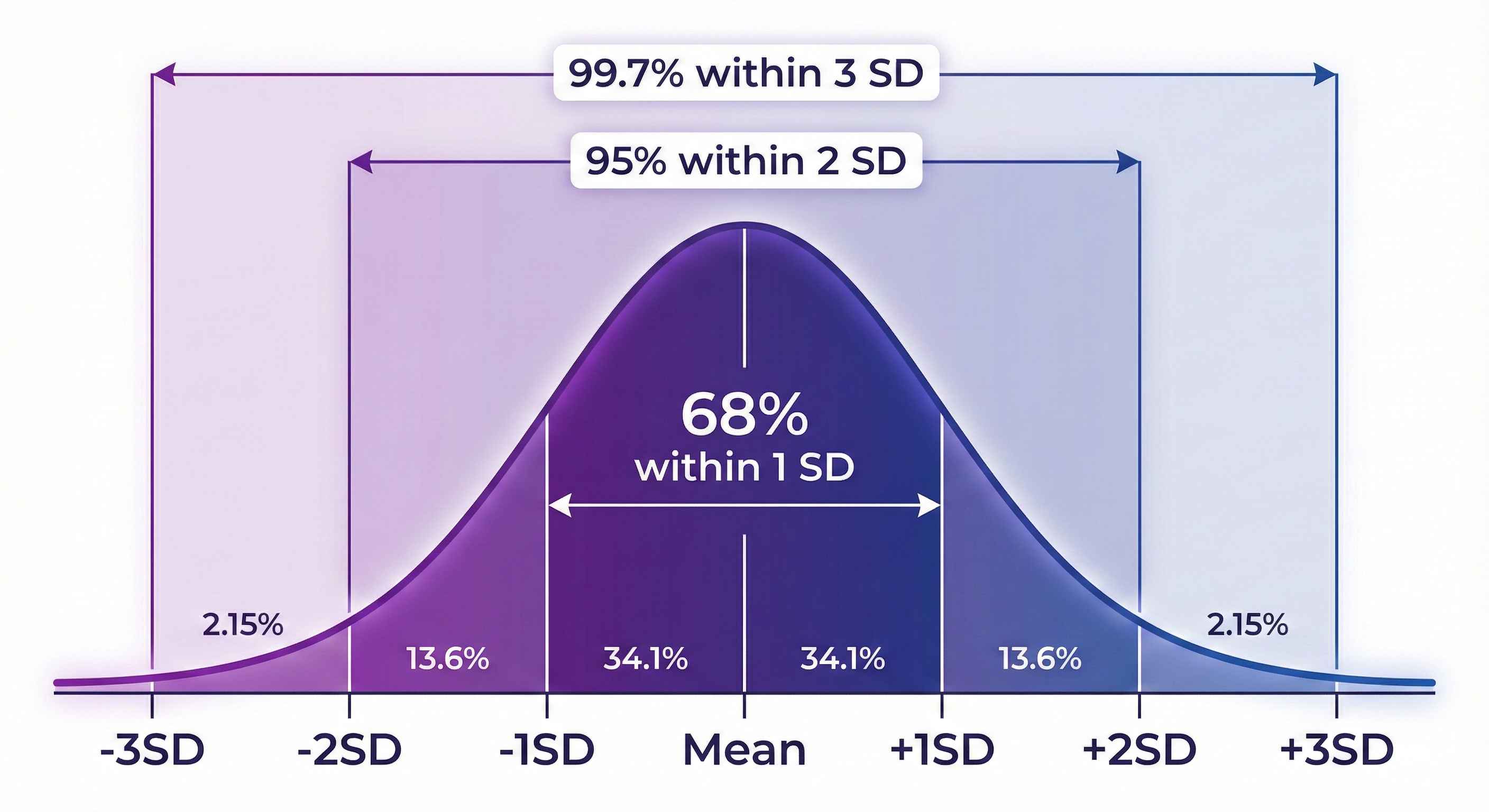
68-95-99 Rule

For normal data:

68% of data falls within 1 SD of mean
95% of data falls within 2 SD of mean
99.7% of data falls within 3 SD of mean

Example: If mean = 100, SD = 15

68% of values are between 85-115
95% of values are between 70-130

Quick Comparison

Measure	Formula	Best For
Range	Max - Min	Quick overview
Standard Deviation	√Variance	Most analysis
Variance	Avg of squared differences	Statistical calculations

3 rows

Cheat Sheet

Measure	Excel	Python
Range	=MAX()-MIN()	max(data)-min(data)
Variance	=VAR.S()	statistics.variance()
Std Dev	=STDEV.S()	statistics.stdev()

3 rows

Quick Practice

Data: 5, 10, 15, 20, 25 (Mean = 15)

Range = 25 - 5 = 20
SD = 7.9

Tip: Low SD = data points are close to mean. High SD = data is spread out!