Understanding Correlation

What You'll Learn

• Pearson correlation
• Interpreting correlation
• Correlation vs causation
• Common mistakes

Correlation Basics

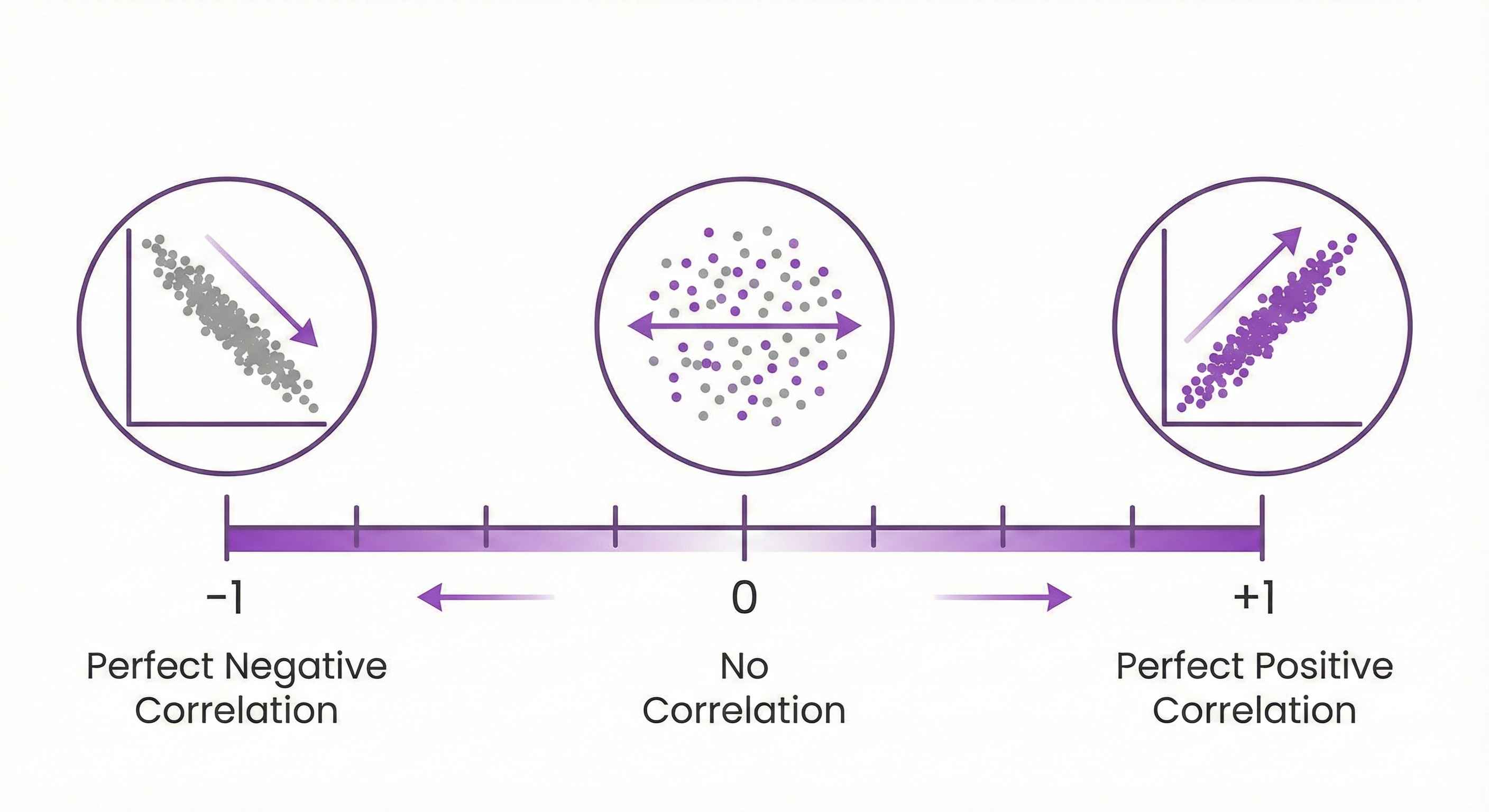
What it measures: Strength of linear relationship between two variables

Range: -1 to +1

• +1: Perfect positive correlation
• 0: No correlation
• -1: Perfect negative correlation

Pearson Correlation (r)

Formula: r = Cov(X,Y) / (SD_x × SD_y)

Interpretation:

• r > 0.7: Strong positive
• r = 0.3-0.7: Moderate
• r < 0.3: Weak
• Negative values: Inverse relationship

Excel: =CORREL(X_range, Y_range) Python: df.corr() or scipy.stats.pearsonr(x, y)

Visualizing: Scatter Plots

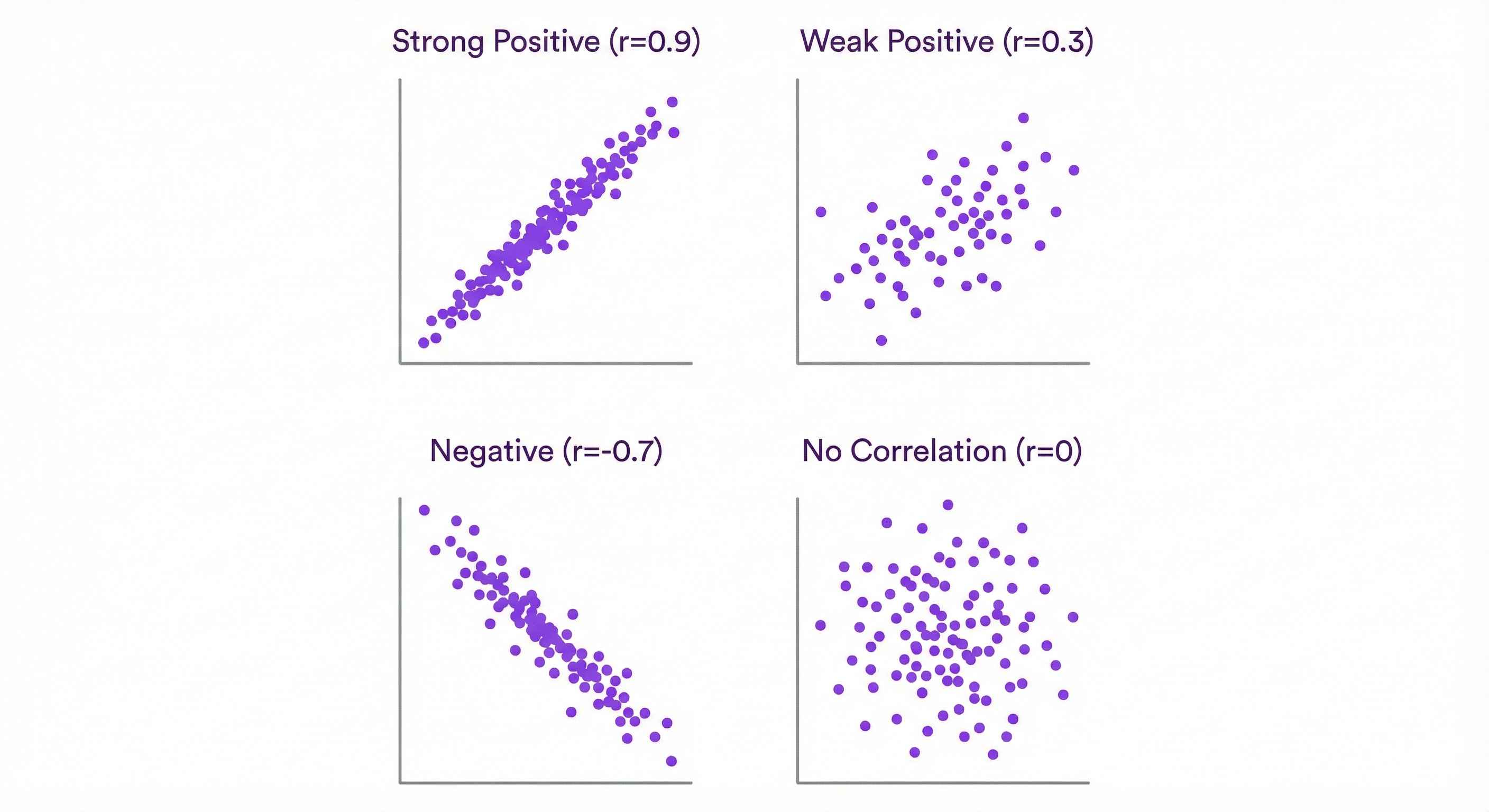
Always plot your data!

Patterns:

• Upward slope: Positive correlation
• Downward slope: Negative correlation
• Cloud: No correlation
• Curve: Nonlinear (correlation misleading!)

Correlation ≠ Causation

Classic mistake: Correlation doesn't prove one causes the other!

Examples:

• Ice cream sales & drowning (both caused by summer!)
• Shoe size & reading ability in kids (both caused by age!)

Remember: Association ≠ Causation

Limitations

Only measures linear relationship: Could be strong nonlinear but r=0

Sensitive to outliers: One extreme point changes r

Doesn't show direction: X causes Y? Y causes X? Third variable?

Spurious Correlations

Meaningless correlations:

• Nicolas Cage films & pool drownings
• Cheese consumption & bed sheet deaths

Lesson: Don't data mine for correlations!

Practice Exercise

Data: Hours studied: 1, 2, 3, 4, 5 Test score: 60, 70, 75, 85, 90

Calculate correlation coefficient.

Next Steps

Learn about Confounding Variables!

Tip: Correlation is first step, not conclusion!