Model Assumptions

What You'll Learn

• The 4 key assumptions
• How to check them
• What to do if violated

The LINE Assumptions

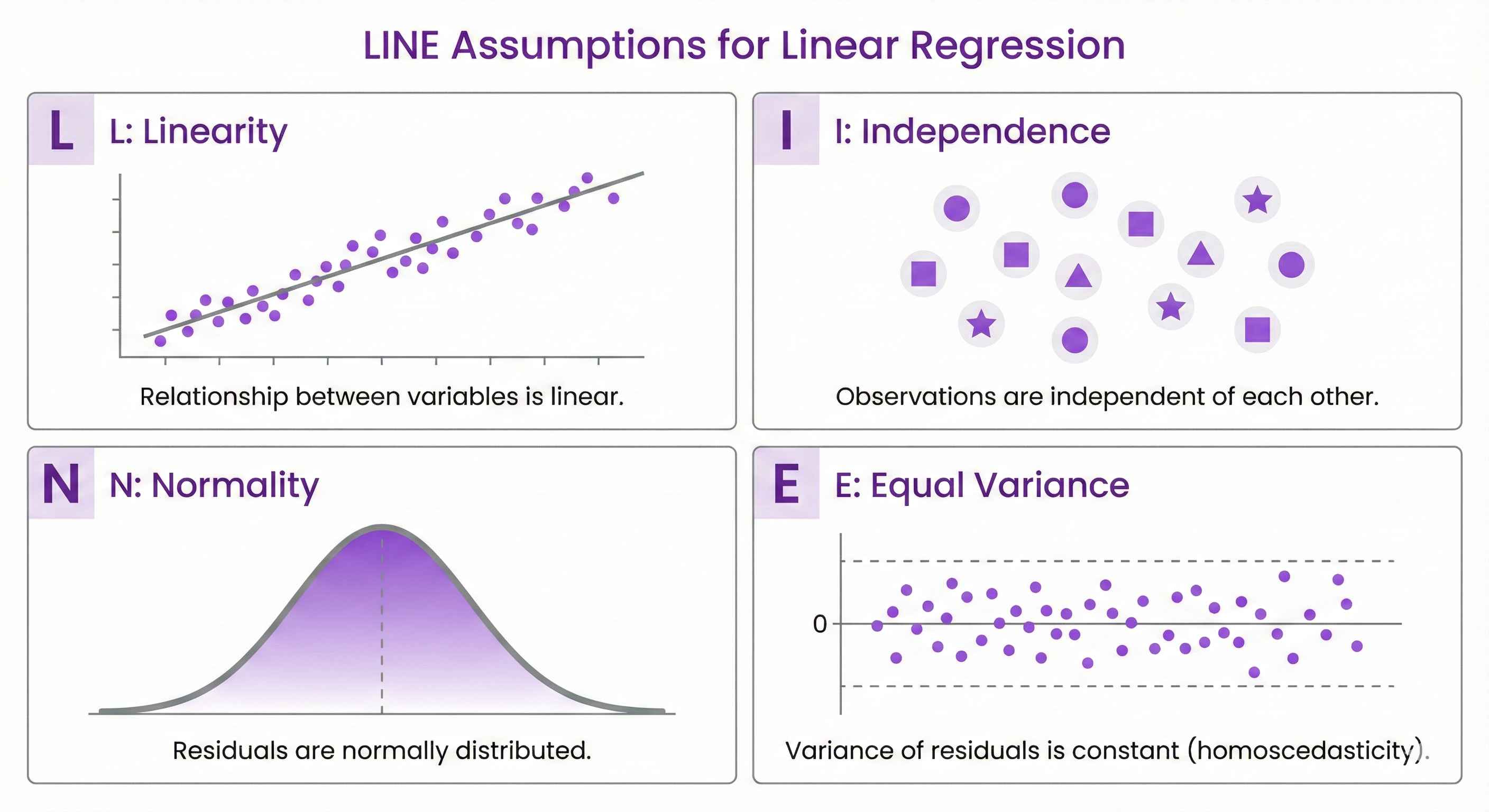
Remember: LINE

L = Linearity (straight line relationship) I = Independence (observations unrelated) N = Normality (residuals bell-shaped) E = Equal variance (constant spread)

1. Linearity

Check: Plot your data - does it follow a line?

Good: Points roughly follow straight line Bad: Curved or zigzag pattern

Fix: Transform data (log, square root) or use curved model

2. Independence

Check: Are observations related?

Violations:

• Time series (today affects tomorrow)
• Groups (students in same class)
• Repeated measures (same person twice)

Fix: Use specialized models for dependent data

3. Normality

Check: Histogram of residuals - bell-shaped?

Good: Bell curve centered at zero Bad: Heavily skewed or multiple peaks

Fix: Transform Y variable or use robust methods

Note: Less critical with large samples!

4. Equal Variance (Homoscedasticity)

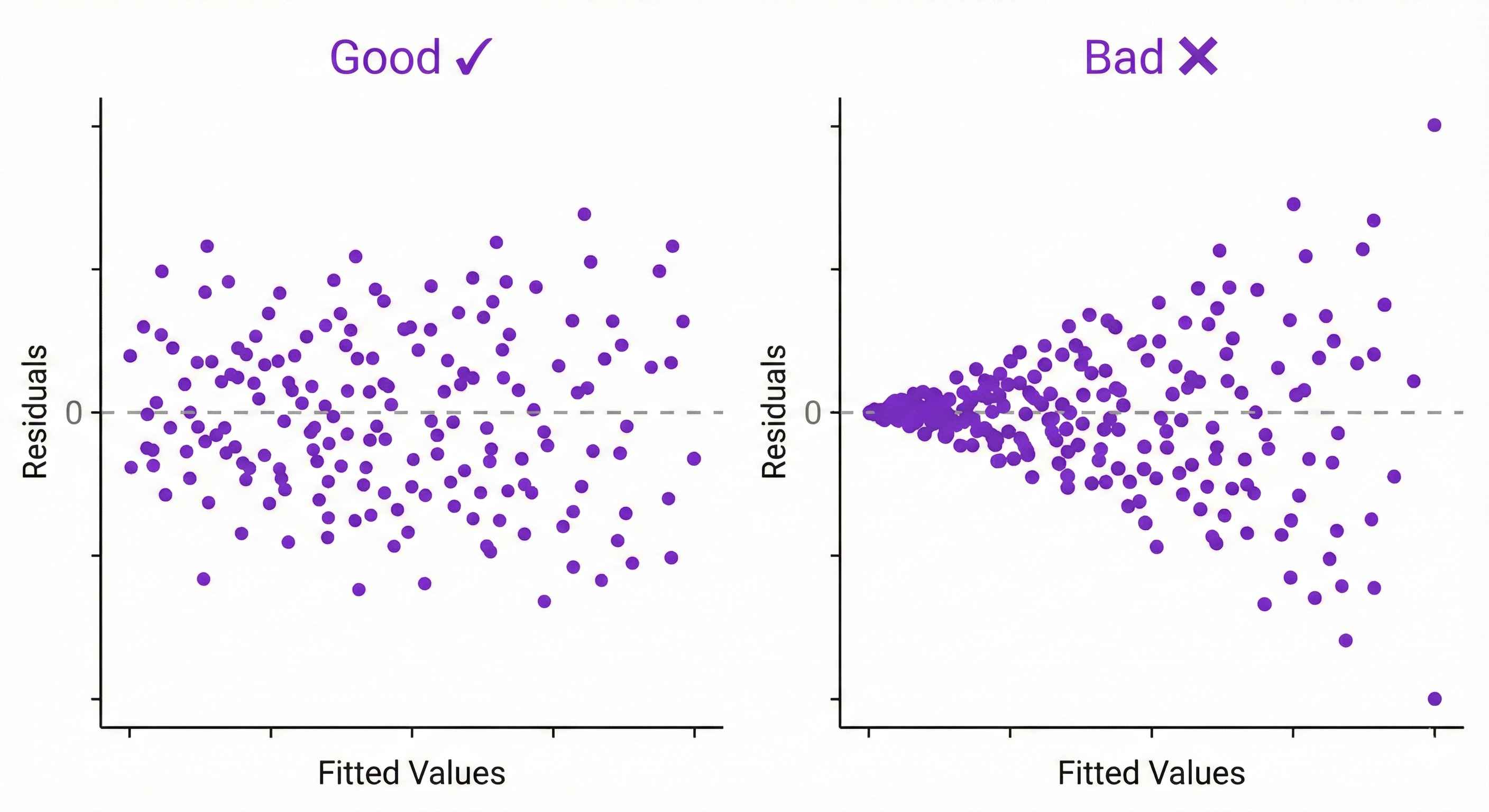
Check: Plot residuals vs predictions

Good: Random scatter, even spread Bad: Funnel shape (spread increases)

Fix: Log transform Y or use weighted regression

Quick Check Checklist

Before trusting your model:

1. ✓ Scatter plot looks linear?
2. ✓ Data points independent?
3. ✓ Residuals roughly bell-shaped?
4. ✓ Even spread in residuals?

If NO to any: Fix it before making predictions!

Common Fixes

Problem: Curved relationship Fix: Try log(Y) or add X²

Problem: Funnel shape Fix: Use log(Y)

Problem: Outliers Fix: Investigate and possibly remove

Practice Exercise

Data: House prices vs square footage

Your job:

1. Make scatter plot
2. Check if it's a straight line
3. Run regression
4. Plot residuals
5. Fix any issues

Real Example

Salary prediction:

• Started with: Salary = β₀ + β₁(Years)
• Found: Funnel pattern (big earners vary more)
• Fixed: log(Salary) = β₀ + β₁(Years)
• Result: Much better fit!

Next Steps

Learn about Multiple Regression!

Tip: Check assumptions BEFORE trusting your regression results!